В1. В. Куб. Уровень B. Помощь. Построить сечение куба плоскостью, проходящей через точки А,К и Е.Найдите линию пересечения этой плоскости а) с ребром ВВ1; б)плоскостью (СС1D). Е. С1. К. А1. D1. С. D. А. Меню.
Слайд 4 из презентации «Задачи на построение сечений» . Размер архива с презентацией 198 КБ.Геометрия 10 класс
краткое содержание других презентаций«Определение двугранных углов» - Точка на ребре может быть произвольная. Построим BK. Задача. Решение задач. Плоскость М. Ромб. Определение и свойства. Где можно увидеть теорему трёх перпендикуляров. Концы отрезка. Проведем луч. Свойства. Двугранные углы в пирамидах. Точки М и К лежат в разных гранях. Отрезки АС и ВС. Свойство трёхгранного угла. Определение. Двугранные углы. Найдите угол. Провести перпендикуляр. Градусная мера угла.
«Примеры центральной симметрии» - Плоскость. Аксиомы планиметрии. Точки. Центральная симметрия. Один центр симметрии. Гостиница «Прибалтийская». Капсула поезда. Длина отрезка. Примеры симметрии в растениях. Центральная симметрия в архитектуре. Ромашка. Отрезок имеет определённую длину. Отрезок. Аксиомы стереометрии и планиметрии. Аксиомы стереометрии. Центральная симметрия в квадратах. Центральная симметрия в транспорте. Различные прямые.
«Равносторонние многоугольники» - Октаэдр Октаэдр составлен из восьми равносторонних треугольников. «Эдра» - грань «тетра» - 4 «гекса» - 6 «окта» - 8 «икоса» - 20 «дедека» - 12. Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Октаэдр имеет 8 граней, 6 вершин и 12 ребер. Существует 5 видов правильных многогранников. Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников.
«Применение правильных многогранников» - Многогранники в природе. Теорема Эйлера. Задачи проекта. Использование в жизни. Мир правильных многогранников. Многогранники в архитектуре. Многогранники в искусстве. Многогранники в математике. Архимед. Кеплер. Теория многогранников. Золотая пропорция в додекаэдре и икосаэдре. Заключение. Платон. Группа «Историки». Евклид. История возникновения правильных многогранников. Взаимосвязь «золотого сечения» и происхождения многогранников.
«Тела Платона» - Октаэдр. Тела Платона. Гексаэдр. Правильные многогранники. Платон. Додекаэдр. Дуальность. Икосаэдр. Правильные многогранники или тела Платона. Тетраэдр.
«Методы построения сечений многогранников» - Правила для самоконтроля. Постройте сечение призмы. Корабль. Многоугольники. Простейшие задачи. Взаимное расположение плоскости и многогранника. Точки пересечения. Пересекаются ли прямые. Разрезы образовали пятиугольник. Делаем разрезы. Законы геометрии. Аксиоматический метод. След секущей плоскости. Задача. Секущая плоскость. Построение сечений многогранников. Сечение. Опрос. Любая плоскость. Сечения параллелепипеда.
Задачи на Построение сечений кубаD1
С1
Е
А1
B1
D
А
F
B
С
Проверочная работа.
1 вариант2 вариант
1. тетраэдр
1. параллелепипед
2. Свойства параллелепипеда
Секущей плоскостью куба называется любая плоскость, по обе стороны от которой имеются точки данного куба.
Секущаяплоскость пересекает грани куба по
отрезкам.
Многоугольник, сторонами которого являются
данные отрезки, называется сечением куба.
Сечениями куба могут быть треугольники,
четырёхугольники, пятиугольники и
шестиугольники.
При построении сечений следует учитывать тот
факт, что если секущая плоскость пересекает две
противоположные грани по каким-то отрезкам, то
эти отрезки параллельны. (Объясните почему).B1
C1
D1
A1
M
K
ВАЖНО!
B
С
D
ЕслиAсекущая плоскость пересекает
противоположные грани, то она
K DCC1
пересекает их по параллельным
M BCC1
отрезкам.
три данные точки, являющиеся серединами рёбер. Найдите периметр сечения, если ребро ку
Постройте сечение куба плоскостью, проходящей черезтри данные точки, являющиеся серединами рёбер.
Найдите периметр сечения, если ребро куба равно а.
D1
N
K
А1
D
А
С1
B1
M
С
B
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся его вершинами. Найдите периметр сечения, если ребро куба
Постройте сечение куба плоскостью, проходящей черезтри данные точки, являющиеся его вершинами. Найдите
периметр сечения, если ребро куба равно а.
D1
С1
А1
B1
D
А
С
B
D1
С1
А1
М
B1
D
А
С
B
Постройте сечение куба плоскостью, проходящей через три данные точки. Найдите периметр сечения, если ребро куба равно а.
D1С1
А1
B1
N
D
А
С
B
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер.
С1D1
B1
А1
K
D
С
N
Е
А
M
B
Общеобразовательная школа І-ІІІ ступеней №2
отдела образования администрации города Кировское
«Сечение куба плоскостью
и практическое их применение в задачах».
Подготовила учитель математики
учитель-методист
Чумакова Г.В.
2015 г.
Введение:
Задачи на построение сечений многогранников занимают значительное место как школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений.
Основными действиями, составляющими метод построения сечений, являются нахождение точки пересечения прямой с плоскостью, построение линий пересечения двух плоскостей, построение прямой параллельной плоскости, построение прямой перпендикулярной плоскости.
Проиллюстрирую построение сечения на одной задаче из школьного курса математики:
№1. Постройте хотя бы два сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью АМ 1 С, если точка М 1 движется по отрезку ВВ 1 от В до В 1 . Найдите границы измерения высоты сечения, проведённой из точки М 1 .
Решение: Построим два требуемых сечения, взяв точку М
1
ближе к точке В, а точку М
2
ближе к В
1
. Оба сечения показаны на рисунке.В начале движения когда точка М
1
только отошла от точки В
1
, сечение представляет собой треугольник с основанием АС и высотой М
1
О, которая чуть больше отрезка ВО, т.е.
 Если точка М
1
займёт положение М
2
расположенной очень близко к точке В
1
, то
Если точка М
1
займёт положение М
2
расположенной очень близко к точке В
1
, то
 АМ
2
С почти совпадёт с
АМ
2
С почти совпадёт с
 АВ
1
С, а его высота М
1
О – с отрезком В
1
О, длина которого равна
АВ
1
С, а его высота М
1
О – с отрезком В
1
О, длина которого равна  (ОВ 1 =
(ОВ 1 = =
= ).
).
Отсюда по соображениям непрерывности делаем вывод: 
Особо следует посмотреть, что произойдёт, если точка М 1 займёт положение вершины В.
№2. Построить сечение куба плоскостью, проходящей через три точки А 1 , E и L , лежащие на рёбрах куба.

Плоскости граней A 1 ADD 1 и DD 1 C 1 C пересекаются по прямой DD 1 , а плоскости граней A 1 B 1 C 1 D 1 u DD 1 C 1 C – по прямой D 1 C 1 . Соединив точки А и Е, получим прямую пересечения секущей плоскости с плоскостью грани AA 1 D 1 D , а продолжив её, найдём точку N , принадлежащую трём плоскостям: плоскости сечения и плоскостям граней AA 1 D 1 D u DD 1 C 1 C .
Аналогично найдём точку М, общую трём плоскостям: плоскости сечения и плоскостям граней A 1 B 1 C 1 D 1 u DD 1 C 1 C . Таким образом, точки N u M принадлежат секущей плоскости и плоскости DD 1 C 1 C ; прямая MN – линия пересечения плоскости сечения с плоскостью грани DD 1 C 1 C , а F и K – точки пересечения её с рёбрами куба CD u CC 1 . Последовательно соединив прямыми точки A 1 , E , F , K u L , получаем пятиугольник A ! EFKL , который и даст нам искомое сечение.








При построении сечения куба плоскостью Х при произвольном расположении точек в сечении получается: треугольник, трапеция, прямоугольник, пятиугольник или шестиугольник. Естественно возник вопрос, как вид сечения зависит от вида расположения точек задающих это сечение
Я решил провести исследование, цель которого является выяснение.
Построить сечения куба плоскостью, когда заданы три точки принадлежащие рёбрам с одной вершиной.



Взяты три точки A 1 , D , C 1 , которые принадлежат вершине D 1 , а сами являются вершинами куба.
В сечении получился равносторонний треугольник, так как A 1 C 1 , A 1 D u DC 1 – диагонали граней этого куба.
Три точки: A 1 u C 1 – вершины куба, а точка F принадлежит ребру куба DD 1 . Точки принадлежат прямым выходящим из вершины D 1 .
В сечении получился равнобедренный треугольник, так как F равноудалена от точек A 1 u C 1 .
Три точки: A 1 u C 1 – вершины куба, а точка F принадлежит прямой ребра куба DD 1 . Точки принадлежат прямым выходящим из одной вершины D 1 .
В сечении получается равнобедренная трапеция, так как F равноудалена от точек A 1 u C 1 , то есть LA 1 =KC 1 .



Три точки принадлежащие рёбрам с одной вершиной D 1 . Точки F u M принадлежат продолжениям рёбер D 1 D u D 1 C соответственно, а точка A 1 является вершиной куба.
В сечении получился пятиугольник A 1 KLNG .
Взяты три точки F , M u Q так, что лежат на продолжении рёбер D 1 D , D 1 C 1 , и D 1 A 1 соответственно.
В сечении получился шестиугольник KLNGJH .
Три точки лежат на рёбрах с одной вершиной D 1 .
В сечении получился произвольный треугольник, но если точки расположить так чтобы D 1 Q =D 1 M =D 1 F , то есть если они были бы равноудалены от вершины D 1 то в сечении получился бы равносторонний треугольник.

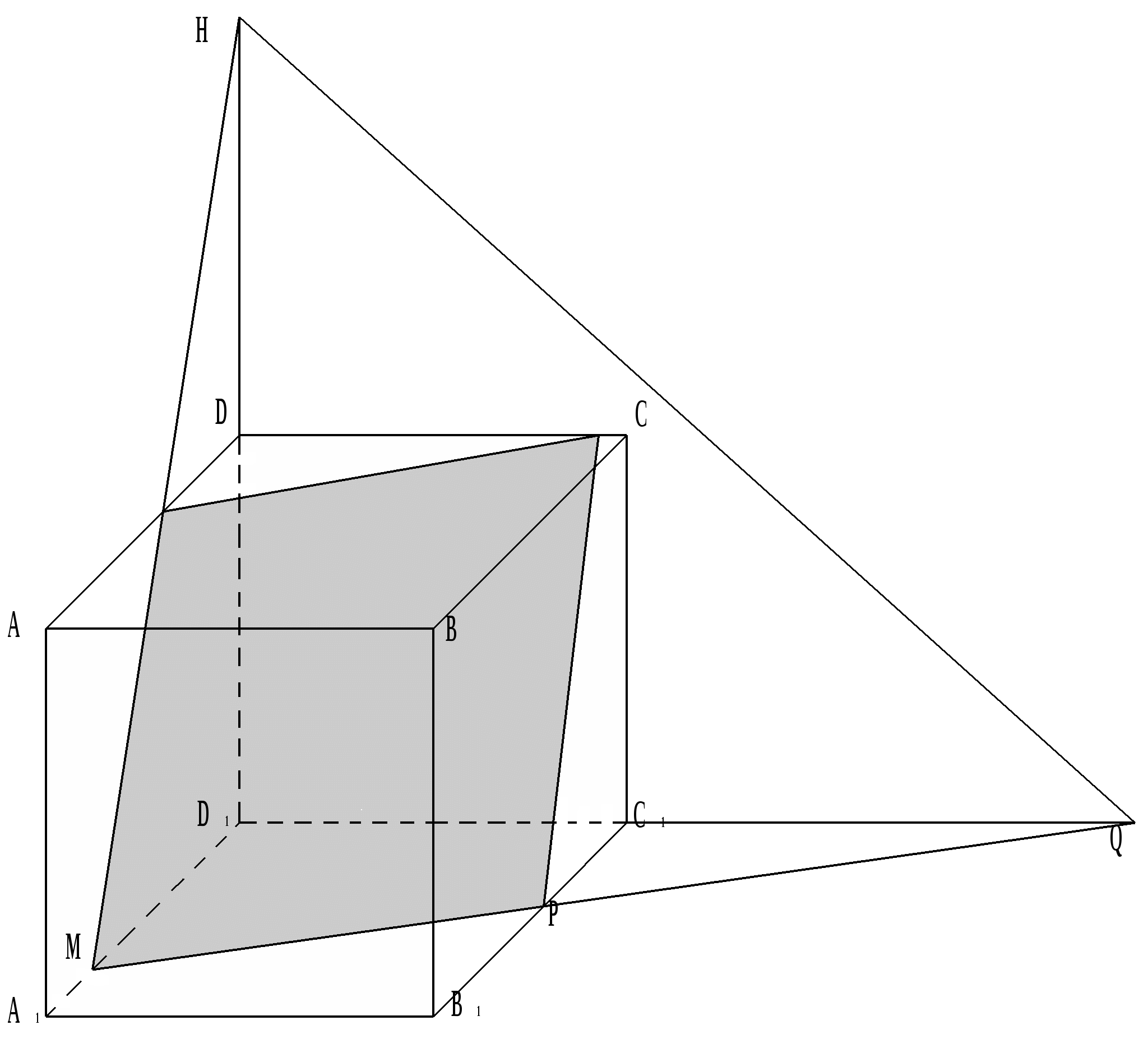
Секущая плоскость задана точками Н, Q и M . В сечении получается параллелограмм, так как KC ││ MP и MK ││ PC по теореме о пересечении двух параллельных плоскостей третьей.

Если точки H , Q и M , задают секущую плоскость, удаленные от D , на расстоянии 2a , где а – для ребра куба, то в сечении получается правильный треугольник ACB 1 .
Вывод: три задающих сечение точки принадлежат трём рёбрам куба с общей вершиной или являются их продолжением, то в сечении получается: треугольник, пятиугольник, шестиугольник трапеция, параллелограмм.
Построение сечения куба плоскостью, когда заданы три точки, две из которых лежат на смежных рёбрах, а третья точка лежит на ребре не смежном с ними.


Три точки M , K u F , взяты так что M u F принадлежат рёбрам с одной вершиной A 1 , а точка K лежит на ребре не смежным с ними.
В сечении получается прямоугольник, так как А 1 М=D
1 K
и по теореме о трёх перпендикулярах можно доказать что MKLF
– прямоугольник., а если А 1 М D
1 K
, то может получится трапеция или пятиугольник.
D
1 K
, то может получится трапеция или пятиугольник.



Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A 1, а точка N принадлежит ребру CC 1 , не смежному сними. K , L u N середины рёбер A 1 A , A 1 B 1 u CC 1 – соответственно.
В сечении получается правильный шестиугольник KLGNHM
Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A 1, а точка T принадлежит ребру DC .
В сечении получается шестиугольник KLFRTZ .


Три точки взяты так, что K u L принадлежат рёбрам куба с одной вершины A 1 , а точка M ребре DD 1 .
В сечении получается трапеция LKQM .
Три точки K u L которые принадлежат рёбрам с одной вершиной A 1 .и точка R которая лежит на ребре BC .
В сечении получается пятиугольник KLFRT .
Вывод: Если секущая плоскость задана тремя точками, две из которых лежат на смежных рёбрах, а третья на ребре не смежном с ними, то в сечении может получиться прямоугольник, пятиугольник, шестиугольник, трапеция.
В сечении куба параллелограмм и его частные случаи.



Точки T
, H
, J
задающие сечение расположены так, что TH AD
, HJ
AD
, HJ AD
. В сечении получается квадрат HTKJ
.
AD
. В сечении получается квадрат HTKJ
.
Сечение задано точками C , F , L , причём DF =FD 1 , BL =LB 1 . В сечении получается ромб AFCL .
Сечение задано точками C , G , H . B 1 H =DG . В сечении параллелограмм A 1 GCH.
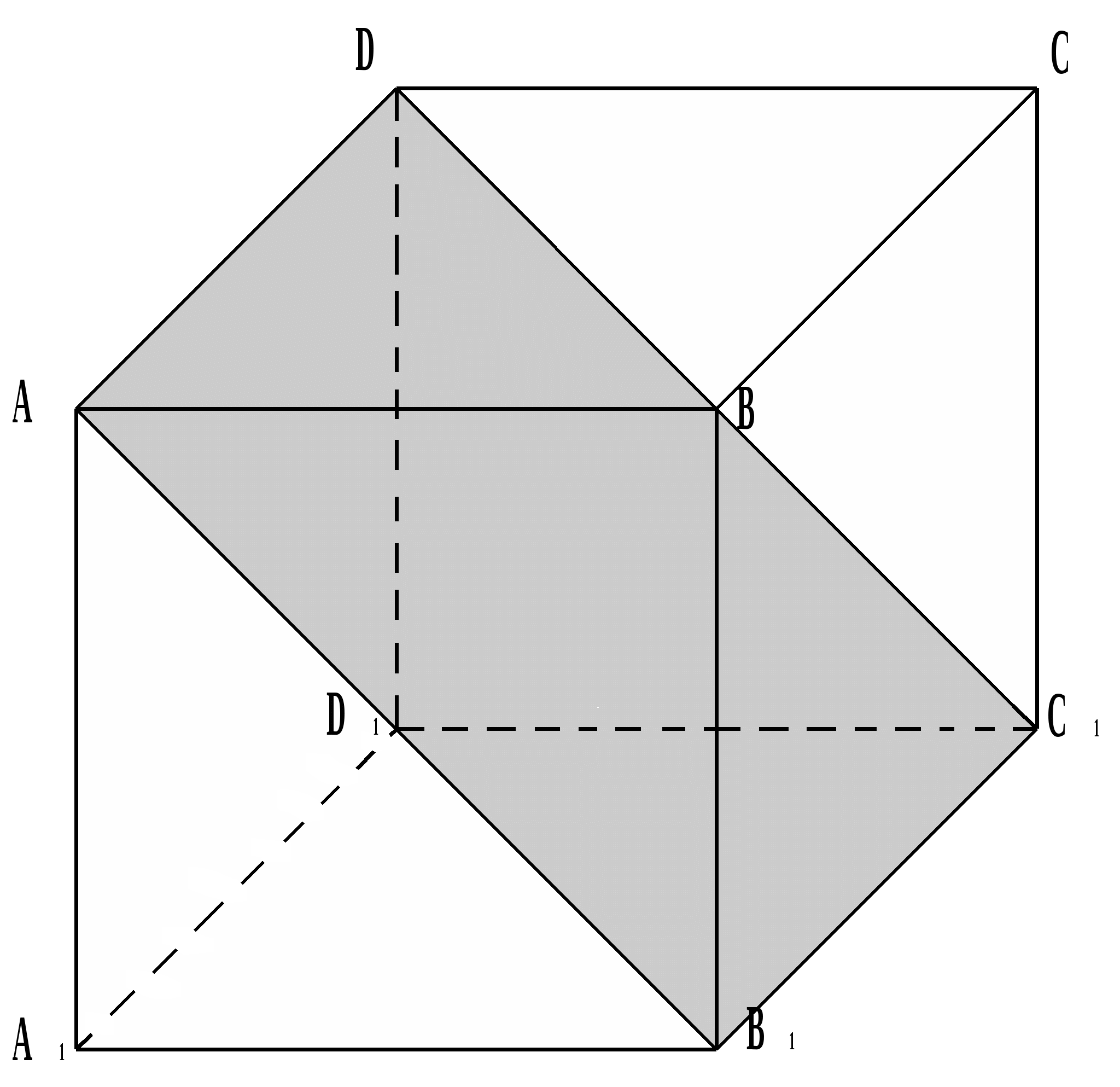
Точки задающие сечение являются вершинами куба A , D , C 1 . В сечении получается прямоугольник
В сечении куба правильные многоугольники



Треугольник АВВ 1 равносторонний, так как его стороны это диагонали граней куба.
Треугольник КМТ равносторонний, так как КВ=МВ=ТВ.
КМТЕ – квадрат, так как сечение задано точками М, К, Е и МК AD
, EK
AD
, EK AD
.
AD
.
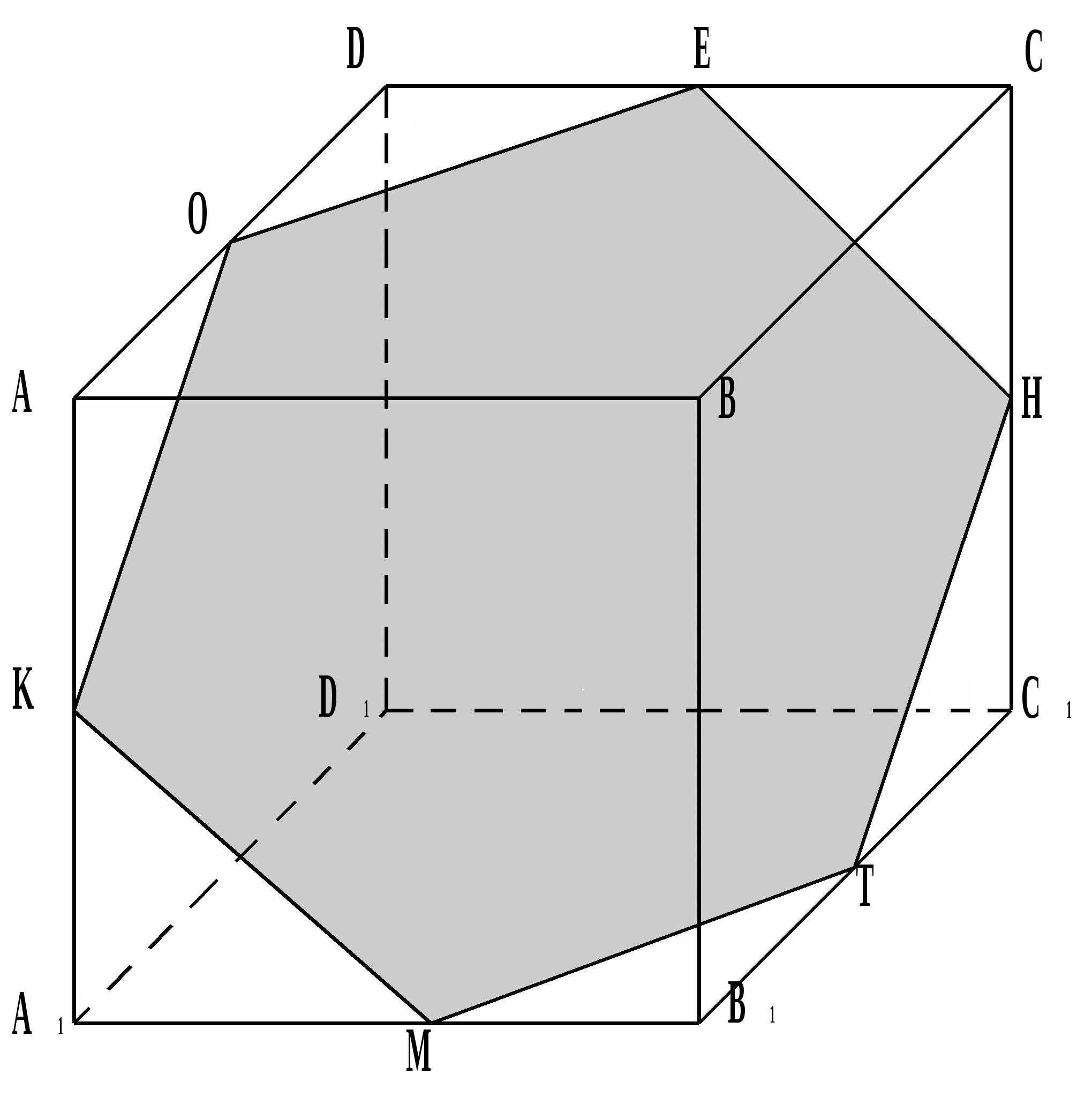
В сечении правильный шестиугольник КМТНЕО, так как точки Н, Е, К задающие сечение являются серединами рёбер СС 1 , DC , АА 1 соответственно.
Куб и несколько задач по стереометрии с ЕГЭ.
В пособии “ЕГЭ 2005. Математика. Типовые тестовые задачи” (Корникова Т. А. и др.) Содержит 10 задач (С4) по стереометрии, объединенных общей идеей: дана треугольная призма АВСА
1
В
1
С
1
стороны основания АВ и ВС взаимно перпендикулярны и перпендикулярны ребру ВВ
1
, АВ=ВС=ВВ
1
, вершина А является вершиной конуса (или центром одного из оснований цилиндра, или центром сферы), основание конуса (сфера или второе основание цилиндра) проходит через середину одного ребра призмы, длина его известна. Надо найти объем или поверхность конуса (сферы, цилиндра).

Общий пример решения:
Данную призму дополнить до куба. Шестиугольник DEFKLM – сечение куба плоскостью основания конуса, окружность которого проходит через середину А 1 В 1 , А – вершина конуса, или

DEFKLM – сечение куба плоскостью основания цилиндра, окружность которого проходит через середину А 1 В 1 , А – центр второго основания цилиндра, или это сечение куба плоскостью большого круга сферы с центром А, сфера которого проходит через середину А 1 В 1 .
Шестиугольник
DEFKLM
– сечение куба плоскостью, проходящей через середину рёбер А
1
В
1
, ВВ
1
, ВСЖ при построении получаются точки
K
,
L
,
M
, которые являются серединами соответствующих рёбер. Стороны этого шестиугольника являются гипотенузами треугольников
DB
1
E
,
EBF
,
FCK
,
KQL
,
LRM
,
MA
1
D
, катеты которых равны половине ребра куба. Тогда центр этого шестиугольника является центром описанной около него окружности, которая пересекает рёбра куба в точках
D
,
E
,
F
,
K
,
L
и М, радиус этой окружности  , где А
1
В
1
=
а
.
, где А
1
В
1
=
а
.
AO  EL,
т
.
к
.
EL,
т
.
к
.
 EAL
– равнобедренный:
AL
=
AE
.
EAL
– равнобедренный:
AL
=
AE
.
(
 ABE
u
ABE
u
 EAL
– прямоугольные,
AB
=
AQ
=
а,
BE
=
LQ
=
)
EAL
– прямоугольные,
AB
=
AQ
=
а,
BE
=
LQ
=
)
EO
=OL
как середина диагонали ЕL
шестиугольника DEFKLM
, т. е. АО – медиана,а по свойствам равнобедренного треугольника и высота. Аналогично доказывается АО  DK
. Так как АО перпендикулярна к двум пересекающимся прямым плоскости шестиугольника, то АО перпендикулярна ко всей плоскости.
DK
. Так как АО перпендикулярна к двум пересекающимся прямым плоскости шестиугольника, то АО перпендикулярна ко всей плоскости.
Если А – вершина конуса то АО – его высота, если А – центр второго основания цилиндра, то АО- высота цилиндра.
 АВС: АС=
АВС: АС= ,
P
– точки пресечения диагоналей основания куба, АР=
,
P
– точки пресечения диагоналей основания куба, АР= , РР
1
=АА
1
=
а
. ОР=РР
1
= , тогда из прямоугольного
, РР
1
=АА
1
=
а
. ОР=РР
1
= , тогда из прямоугольного
 РОА АО=
РОА АО= . И так АО=
. И так АО= .
.
Тогда, если идёт речь о конусе:
 =
=

 (из
(из  ).
).


Ответ: 

Если речь идёт цилиндре:

Ответ: 

Если речь идёт о сфере:


Ответ: 

Корникова Т. А. и др. типовые тестовые задания. ЕГЭ – 2005
Вариант 6.
Задача. Даны призма АВСА 1 В 1 С 1 и цилиндр. Стороны АВ и ВС основания призмы перпендикулярны ребру ВВ 1 и взаимно перпендикулярны. Центром основания цилиндра служит точка А 1 окружность второго основания проходит через середину ребра А 1 В 1 .
Найдите площадь полной поверхности цилиндра, если ВВ 1 =АВ=ВС=10. Найдите его объём.
Решение:

.  .
.
Определение
Сечение - это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”
.
Важные определения
1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.
4. Две плоскости параллельны, если они не имеют общих точек.
5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен \(90^\circ\) .
6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
7. Две плоскости называются перпендикулярными, если угол между ними равен \(90^\circ\) .
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая \(a\) , не лежащая в плоскости \(\pi\) , параллельна некоторой прямой \(p\) , лежащей в плоскости \(\pi\) , то она параллельна данной плоскости.
2. Пусть прямая \(p\) параллельна плоскости \(\mu\) . Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\) , то линия пересечения плоскостей \(\pi\) и \(\mu\) - прямая \(m\) - параллельна прямой \(p\) .

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\) , то линии пересечения плоскостей также параллельны:
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

5. Пусть прямая \(l\) лежит в плоскости \(\lambda\) . Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\) , не лежащей на прямой \(l\) , то прямые \(l\) и \(s\) скрещиваются.

6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
7. Теорема о трех перпендикулярах.
Пусть \(AH\) – перпендикуляр к плоскости \(\beta\) . Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\) . Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.

8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

Для этого из двух произвольных точек \(A\) и \(B\) прямой \(a\) проведем перпендикуляры на плоскость \(\mu\) – \(AA"\) и \(BB"\) (точки \(A", B"\) называются проекциями точек \(A,B\) на плоскость). Тогда прямая \(A"B"\) – проекция прямой \(a\) на плоскость \(\mu\) . Точка \(M=a\cap A"B"\) и есть точка пересечения прямой \(a\) и плоскости \(\mu\) .
Причем заметим, что все точки \(A, B, A", B", M\) лежат в одной плоскости.
Пример 1.
Дан куб \(ABCDA"B"C"D"\) . \(A"P=\dfrac 14AA", \ KC=\dfrac15 CC"\) . Найдите точку пересечения прямой \(PK\) и плоскости \(ABC\) .
Решение
1) Т.к. ребра куба \(AA", CC"\) перпендикулярны \((ABC)\) , то точки \(A\) и \(C\) - проекции точек \(P\) и \(K\) . Тогда прямая \(AC\) – проекция прямой \(PK\) на плоскость \(ABC\) . Продлим отрезки \(PK\) и \(AC\) за точки \(K\) и \(C\) соответственно и получим точку пересечения прямых – точку \(E\) .

2) Найдем отношение \(AC:EC\) . \(\triangle PAE\sim \triangle KCE\) по двум углам (\(\angle A=\angle C=90^\circ, \angle E\) – общий), значит, \[\dfrac{PA}{KC}=\dfrac{EA}{EC}\]
Если обозначить ребро куба за \(a\) , то \(PA=\dfrac34a, \ KC=\dfrac15a, \ AC=a\sqrt2\) . Тогда:
\[\dfrac{\frac34a}{\frac15a}=\dfrac{a\sqrt2+EC}{EC} \Rightarrow EC=\dfrac{4\sqrt2}{11}a \Rightarrow AC:EC=4:11\]
Пример 2.
Дана правильная треугольная пирамида \(DABC\) с основанием \(ABC\) , высота которой равна стороне основания. Пусть точка \(M\) делит боковое ребро пирамиды в отношении \(1:4\) , считая от вершины пирамиды, а \(N\) – высоту пирамиды в отношении \(1:2\) , считая от вершины пирамиды. Найдите точку пересечения прямой \(MN\) с плоскостью \(ABC\) .
Решение
1) Пусть \(DM:MA=1:4, \ DN:NO=1:2\)
(см. рисунок). Т.к. пирамида правильная, то высота падает в точку \(O\)
пересечения медиан основания. Найдем проекцию прямой \(MN\)
на плоскость \(ABC\)
. Т.к. \(DO\perp (ABC)\)
, то и \(NO\perp (ABC)\)
. Значит, \(O\)
– точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр \(MQ\)
из точки \(M\)
на плоскость \(ABC\)
. Точка \(Q\)
будет лежать на медиане \(AK\)
.
Действительно, т.к. \(MQ\)
и \(NO\)
перпендикулярны \((ABC)\)
, то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки \(M, N, O\)
лежат в одной плоскости \(ADK\)
, то и точка \(Q\)
будет лежать в этой плоскости. Но еще (по построению) точка \(Q\)
должна лежать в плоскости \(ABC\)
, следовательно, она лежит на линии пересечения этих плоскостей, а это – \(AK\)
.

Значит, прямая \(AK\) и есть проекция прямой \(MN\) на плоскость \(ABC\) . \(L\) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки \(L\) (например, на нашем чертеже точка \(L\) лежит вне отрезка \(OK\) , хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим \(AB=DO=a\) . Тогда медиана \(AK=\dfrac{\sqrt3}2a\) . Значит, \(OK=\dfrac13AK=\dfrac 1{2\sqrt3}a\) . Найдем длину отрезка \(OL\) (тогда мы сможем понять, внутри или вне отрезка \(OK\) находится точка \(L\) : если \(OL>OK\) – то вне, иначе – внутри).
а) \(\triangle AMQ\sim \triangle ADO\) по двум углам (\(\angle Q=\angle O=90^\circ, \ \angle A\) – общий). Значит,
\[\dfrac{MQ}{DO}=\dfrac{AQ}{AO}=\dfrac{MA}{DA}=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \ AQ=\dfrac 45\cdot \dfrac 1{\sqrt3}a\]
Значит, \(QK=\dfrac{\sqrt3}2a-\dfrac 45\cdot \dfrac 1{\sqrt3}a=\dfrac7{10\sqrt3}a\) .
б) Обозначим \(KL=x\)
.
\(\triangle LMQ\sim \triangle LNO\)
по двум углам (\(\angle Q=\angle O=90^\circ, \ \angle L\)
– общий). Значит,
\[\dfrac{MQ}{NO}=\dfrac{QL}{OL} \Rightarrow \dfrac{\frac45 a}{\frac 23a} =\dfrac{\frac{7}{10\sqrt3}a+x}{\frac1{2\sqrt3}a+x} \Rightarrow x=\dfrac a{2\sqrt3} \Rightarrow OL=\dfrac a{\sqrt3}\]
Следовательно, \(OL>OK\) , значит, точка \(L\) действительно лежит вне отрезка \(AK\) .
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\) ).
Пример 3
Дана правильная четырехугольная пирамида \(SABCD\) . Найдите сечение пирамиды плоскостью \(\alpha\) , проходящей через точку \(C\) и середину ребра \(SA\) и параллельной прямой \(BD\) .
Решение
1) Обозначим середину ребра \(SA\) за \(M\) . Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\) . Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\) .

Для того, чтобы плоскость \(\alpha\) была параллельна прямой \(BD\) , она должна содержать некоторую прямую, параллельную \(BD\) . Точка \(O\) находится вместе с прямой \(BD\) в одной плоскости – в плоскости \(BSD\) . Проведем в этой плоскости через точку \(O\) прямую \(KP\parallel BD\) (\(K\in SB, P\in SD\) ). Тогда, соединив точки \(C, P, M, K\) , получим сечение пирамиды плоскостью \(\alpha\) .
2) Найдем отношение, в котором делят точки \(K\) и \(P\) ребра \(SB\) и \(SD\) . Таким образом мы полностью определим построенное сечение.
Заметим, что так как \(KP\parallel BD\) , то по теореме Фалеса \(\dfrac{SB}{SK}=\dfrac{SD}{SP}\) . Но \(SB=SD\) , значит и \(SK=SP\) . Таким образом, можно найти только \(SP:PD\) .
Рассмотрим \(\triangle ASC\) . \(CM, SH\) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении \(2:1\) , считая от вершины, то есть \(SO:OH=2:1\) .

Теперь по теореме Фалеса из \(\triangle BSD\) : \(\dfrac{SP}{PD}=\dfrac{SO}{OH}=\dfrac21\) .
3) Заметим, что по теореме о трех перпендикулярах \(CO\perp BD\) как наклонная (\(OH\) – перпендикуляр на плоскость \(ABC\) , \(CH\perp BD\) – проекция). Значит, \(CO\perp KP\) . Таким образом, сечением является четырехугольник \(CPMK\) , диагонали которого взаимно перпендикулярны.
Пример 4
Дана прямоугольная пирамида \(DABC\) с ребром \(DB\) , перпендикулярным плоскости \(ABC\) . В основании лежит прямоугольный треугольник с \(\angle B=90^\circ\) , причем \(AB=DB=CB\) . Проведите через прямую \(AB\) плоскость, перпендикулярную грани \(DAC\) , и найдите сечение пирамиды этой плоскостью.
Решение
1) Плоскость \(\alpha\) будет перпендикулярна грани \(DAC\) , если она будет содержать прямую, перпендикулярную \(DAC\) . Проведем из точки \(B\) перпендикуляр на плоскость \(DAC\) - \(BH\) , \(H\in DAC\) .
Проведем вспомогательные \(BK\)
– медиану в \(\triangle ABC\)
и \(DK\)
– медиану в \(\triangle DAC\)
.
Т.к. \(AB=BC\)
, то \(\triangle ABC\)
– равнобедренный, значит, \(BK\)
– высота, то есть \(BK\perp AC\)
.
Т.к. \(AB=DB=CB\)
и \(\angle ABD=\angle CBD=90^\circ\)
, то \(\triangle
ABD=\triangle CBD\)
, следовательно, \(AD=CD\)
, следовательно, \(\triangle DAC\)
– тоже равнобедренный и \(DK\perp AC\)
.
Применим теорему о трех перпендикулярах: \(BH\) – перпендикуляр на \(DAC\) ; наклонная \(BK\perp AC\) , значит и проекция \(HK\perp AC\) . Но мы уже определили, что \(DK\perp AC\) . Таким образом, точка \(H\) лежит на отрезке \(DK\) .

Соединив точки \(A\) и \(H\) , получим отрезок \(AN\) , по которому плоскость \(\alpha\) пересекается с гранью \(DAC\) . Тогда \(\triangle ABN\) – искомое сечение пирамиды плоскостью \(\alpha\) .
2) Определим точное положение точки \(N\) на ребре \(DC\) .
Обозначим \(AB=CB=DB=x\) . Тогда \(BK\) , как медиана, опущенная из вершины прямого угла в \(\triangle ABC\) , равна \(\frac12 AC\) , следовательно, \(BK=\frac12 \cdot \sqrt2 x\) .
Рассмотрим \(\triangle BKD\) . Найдем отношение \(DH:HK\) .

Заметим, что т.к. \(BH\perp (DAC)\) , то \(BH\) перпендикулярно любой прямой из этой плоскости, значит, \(BH\) – высота в \(\triangle DBK\) . Тогда \(\triangle DBH\sim \triangle DBK\) , следовательно
\[\dfrac{DH}{DB}=\dfrac{DB}{DK} \Rightarrow DH=\dfrac{\sqrt6}3x \Rightarrow HK=\dfrac{\sqrt6}6x \Rightarrow DH:HK=2:1\]

Рассмотрим теперь \(\triangle ADC\) . Медианы треугольника точной пересечения делятся в отношении \(2:1\) , считая от вершины. Значит, \(H\) – точка пересечения медиан в \(\triangle ADC\) (т.к. \(DK\) – медиана). То есть \(AN\) – тоже медиана, значит, \(DN=NC\) .
Задачи на Построение сечений кубаD1
С1
Е
А1
B1
D
А
F
B
С
Проверочная работа.
1 вариант2 вариант
1. тетраэдр
1. параллелепипед
2. Свойства параллелепипеда
Секущей плоскостью куба называется любая плоскость, по обе стороны от которой имеются точки данного куба.
Секущаяплоскость пересекает грани куба по
отрезкам.
Многоугольник, сторонами которого являются
данные отрезки, называется сечением куба.
Сечениями куба могут быть треугольники,
четырёхугольники, пятиугольники и
шестиугольники.
При построении сечений следует учитывать тот
факт, что если секущая плоскость пересекает две
противоположные грани по каким-то отрезкам, то
эти отрезки параллельны. (Объясните почему).B1
C1
D1
A1
M
K
ВАЖНО!
B
С
D
ЕслиAсекущая плоскость пересекает
противоположные грани, то она
K DCC1
пересекает их по параллельным
M BCC1
отрезкам.
три данные точки, являющиеся серединами рёбер. Найдите периметр сечения, если ребро ку
Постройте сечение куба плоскостью, проходящей черезтри данные точки, являющиеся серединами рёбер.
Найдите периметр сечения, если ребро куба равно а.
D1
N
K
А1
D
А
С1
B1
M
С
B
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся его вершинами. Найдите периметр сечения, если ребро куба
Постройте сечение куба плоскостью, проходящей черезтри данные точки, являющиеся его вершинами. Найдите
периметр сечения, если ребро куба равно а.
D1
С1
А1
B1
D
А
С
B
D1
С1
А1
М
B1
D
А
С
B
Постройте сечение куба плоскостью, проходящей через три данные точки. Найдите периметр сечения, если ребро куба равно а.
D1С1
А1
B1
N
D
А
С
B
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер.
С1D1
B1
А1
K
D
С
N
Е
А
M
B
